这次的作业主要涉及分形算法[Chaos game版本]
assignment 0
https://github.com/birdy-C/MIT-6-837/tree/master/Result/assignment0
这个assignment大概就是了解了一下分形相关的知识。之前对于分形的认知只有迭代输出一种。
https://en.wikipedia.org/wiki/Sierpinski_triangle
这里实现用到的实现方式是Chaos game,觉得这种类似于元胞自动机的方式非常的神奇。
主要的问题出在矩阵的运算不熟练,以及对于边界情况的处理。
代码
主要逻辑(不是我写的)
1 | for "lots" of random points (x0, y0) |
然后输入
这是那个sierpinski_triangle的,虽然不是很懂为什么别人加的三角形都是等边三角形
1 | 3 |
所以大概思路就是
1 | for "lots" of random points (x0, y0)//x0 y0在[0,1]之间 |
More
写暂时不写了 码一个思路
figure out the probabilities
这个没懂啥意思
如果是要一个概率可视化的话,在最后统计的时候,现在的方法是把白格子染成黑色,如果变为记录落到这个点几次的话,或者给GRB分量减掉一个定值,就理论上能够得到一个与概率有关的图。越黑代表概率越高。
如果需要具体的数值的话(我觉得这个要求有点高啊),可能和这题的离散化的思路不和……需要借助下面那个的bounding box,暂时能想到的就是落在最后的几个bounding box之中。
determine the bounding box
用边界点确定。
比如现在带入的时候是生成[0,1]之间的随机数,那么在这里就可以直接计算0和1的边界情况。把这四个点进行所有可能的变换组合(生成一棵树)。然后依次连接。
Shrinking and duplication
chaos game
这么一想的话就开始思考chaos game和其他连续的实现有什么区别,其实确定边界点的过程就类似于Shrinking and duplication这一种,并且图完色不会像chaos game那样有(密密麻麻的小黑点)的那种感觉。
- chaos game取随机数会有一定的开销,Shrinking and duplication在计算过程中会随着层数的增加运算量指数上升
- Shrinking and duplication这种的图肯定比chaos game好看……但或许可以说chaos game 从某种程度上反应了概率的分布。
change the color scheme
如果是不同的bounding box内颜色不一样的话,可以尝试一下对不同的选择(也就是不同的到达树的叶结点的路径)编码,然后赋予不同的颜色。
anti-aliasing
在这里实现的时候,直接把float裁成int,可以根据具体float值影响周围的四个格子。
比如落在(100.5,100.5),之前的做法是直接把它取整到(100,100),设为黑色。现在可以考虑把(100,100)(100,101)(101,100)(101,101)四个各种分别设置为(127,127,127)的灰色。如果一个格子被多个点影响,则取小的(影响大的)。
depth-first vs. breadth-first
BF除了能够,增加视觉体验,还有啥用吗(还非常占内存……)
结果
最后实现之后感觉fern的分形真的神奇,因为在看这个图的时候我没想到它的迭代规律那么简单。
1 | 4 |
虽然看起来非常的复杂,但其实并没有更多的变换矩阵。
sierpinski_triangle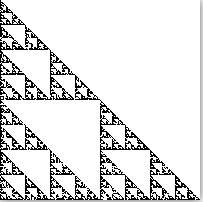
3次迭代
5次迭代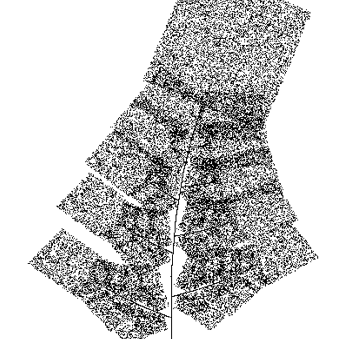
10次
30次